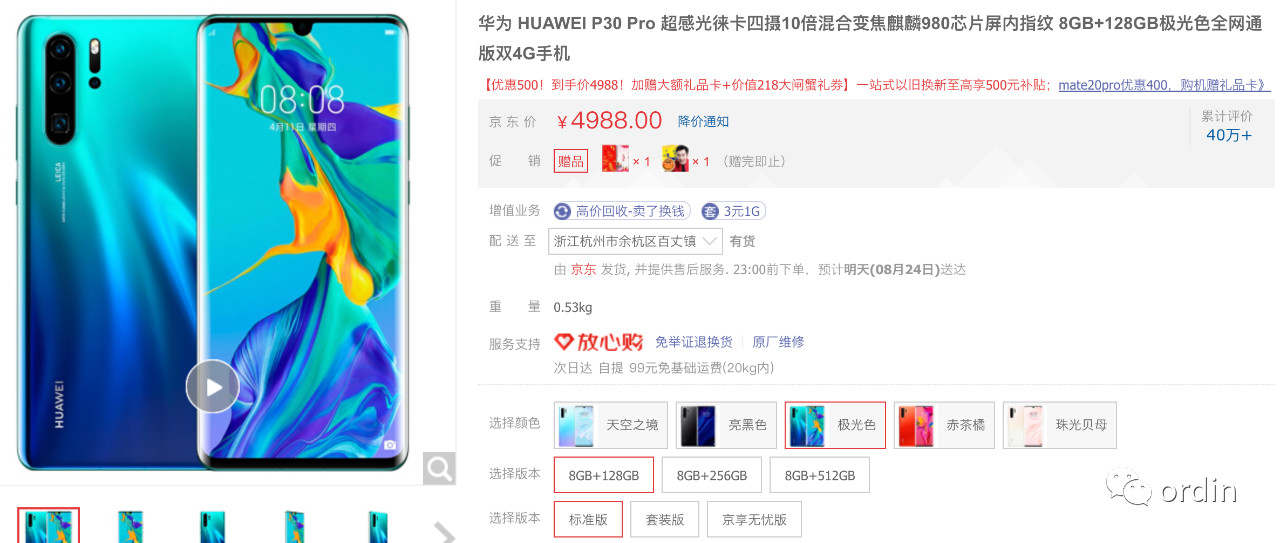
生活中我们经常面临这样的选择。假设你要网购一个华为P30,打开网购页面,你会发现:wc,太贵了,买不起,告辞😂 再仔细一看,按颜色分为:蓝/黑/白...,按内存分:8G+128G/8G+256G...不同的组合价格各不相依,经过不断的抉择,终于选出了一个适合价位get P30一台。那么,问题来了,根据不同的条件组合,一共有多少个版本供我们选择呢?
数学解法
c = 5 * 3 * 3 = 45(种),小儿科不解释。但是用代码如何表示出这45种不同的结果呢?
问题抽象
上面的选择列表可以由以下数据结构表示。
//原始抽象
let select = [
//按颜色分
["天空之境","亮黑色","极光色","赤茶橘","珠光贝母"],
//按内存分
["8G+128G","8G+256G","8G+512G"],
//按套餐分
["标准版","套装版","京享无忧版"]
]
//进一步抽象
let arr = [
[1,2,3,4,5],
[1,2,3],
[1,2,3]
]
//最终抽象得到i行,每行有j个元素的数组集合
let arr = [
[1,2,3,4,5,...],
[1,2,3,...],
[1,2,3,...],
...
[1,...]
]
问题分析
现在的问题,就是如何计算出数组arr的所有组合结果。如:每个分类我们都选第一种,得到组合1,1,1...
从易到难
2组选择集
//选择数组
let arr = [
[1,2],
[1,2]
]
//期望值
let results = [
'1,1',
'1,2',
'2,1',
'2,2'
]
//编码实现
let arr = [
[1, 2],
[1, 2]
]
//结果集
let results = []
//单次结果集
let result = []
let i = 0
for (let j = 0; j < arr[i].length; j++) {
//记录第一组选择的元素
result[i] = arr[i][j]
//遍历第二组选择的元素
for (let k = 0; k < arr[i + 1].length; k++) {
//记住第二组的元素
result[i + 1] = arr[i + 1][k];
//将一种组合放入结果集中
results.push(result.join(","))
}
}
//[ '1,1', '1,2', '2,1', '2,2' ]
console.log(results)
3组选择集
//选择数组
let arr = [
[1, 2],
[1, 2],
[1, 2, 3]
]
//期望值
let results = [
'1,1,1',
'1,1,2',
'1,1,3',
'1,2,1',
'1,2,2',
'1,2,3',
'2,1,1',
'2,1,2',
'2,1,3',
'2,2,1',
'2,2,2',
'2,2,3'
]
//编码实现
let arr = [
[1, 2],
[1, 2],
[1, 2, 3]
]
let results = []
let result = []
let i = 0
for (let j = 0; j < arr[i].length; j++) {
//记录第一组选择的元素
result[i] = arr[i][j]
//遍历第二组选择的元素
for (let k = 0; k < arr[i + 1].length; k++) {
//记住第二组的元素
result[i + 1] = arr[i + 1][k];
for (let p = 0; p < arr[i + 2].length; p++) {
//记住第三组的元素
result[i + 2] = arr[i + 2][p];
//将一种组合放入结果集中
results.push(result.join(","))
}
}
}
//["1,1,1","1,1,2","1,1,3","1,2,1","1,2,2","1,2,3","2,1,1","2,1,2","2,1,3","2,2,1","2,2,2","2,2,3"]
console.log(results)
归纳总结
观察上面的举例可知,当有i组选择时,需要有i个遍历。显然我们不会这么搞,面对这种重复的遍历时,我们显然可以用递归法遍历上述循环。使用递归法,最重要的是找到最小递归单元,观察上述实例,显然在第二层循环时,即可使用递归。通过递归,我们很容易得到最终的解决方案。
最终解
//选择集
let arr = [
[1, 2],
[1, 2],
[1, 2, 3]
]
//最终结果集
let results = []
//单次组合结果集
let result = []
//i列选择
let i = 0;
combination(arr, i);
//组合递归函数
function combination(arr, i) {
for (let j = 0; j < arr[i].length; j++) {
//记录第一组选择的元素
result[i] = arr[i][j]
//如果没有到最后一层,则递归遍历
if (i != arr.length - 1) {
//i + 1 :下一层遍历开始
combination(arr, i + 1)
} else {
//最后一层啦,记录结果集
//join函数是为了避免引用传递造成的影响,这里的result是复用
results.push(result.join(","))
}
}
}
//["1,1,1","1,1,2","1,1,3","1,2,1","1,2,2","1,2,3","2,1,1","2,1,2","2,1,3","2,2,1","2,2,2","2,2,3"]
console.log(JSON.stringify(results))
总结
一个复杂的问题往往都是从最简单的情况入手解决的。化繁为简,由简入繁从而解决各种各样的问题。本次算法颇为简单,但是在此记录一下解决的心路历程,也是颇有意义的一件事情。
本站文章除注明转载/出处外,均为本站原创或翻译,转载前请务必署名,转载请标明出处
最后编辑时间为:
2019-09-06